LeetCode558. 四叉树交集

题目描述

本题目来自LeetCode上的『558. 四叉树交集』

二进制矩阵中的所有元素不是 0 就是 1 。

给你两个四叉树，quadTree1 和 quadTree2。其中 quadTree1 表示一个 n * n 二进制矩阵，而 quadTree2 表示另一个 n * n 二进制矩阵。

请你返回一个表示 n * n 二进制矩阵的四叉树，它是 quadTree1 和 quadTree2 所表示的两个二进制矩阵进行 按位逻辑或运算 的结果。

注意，当 isLeaf 为 False 时，你可以把 True 或者 False 赋值给节点，两种值都会被判题机制接受。

四叉树数据结构中，每个内部节点只有四个子节点。此外，每个节点都有两个属性：

val：储存叶子结点所代表的区域的值。1 对应 True，0 对应 False；
isLeaf: 当这个节点是一个叶子结点时为 True，如果它有 4 个子节点则为 False 。

class Node { 
    public boolean val;
    public boolean isLeaf;
    public Node topLeft;
    public Node topRight;
    public Node bottomLeft;
    public Node bottomRight; 
}

我们可以按以下步骤为二维区域构建四叉树：

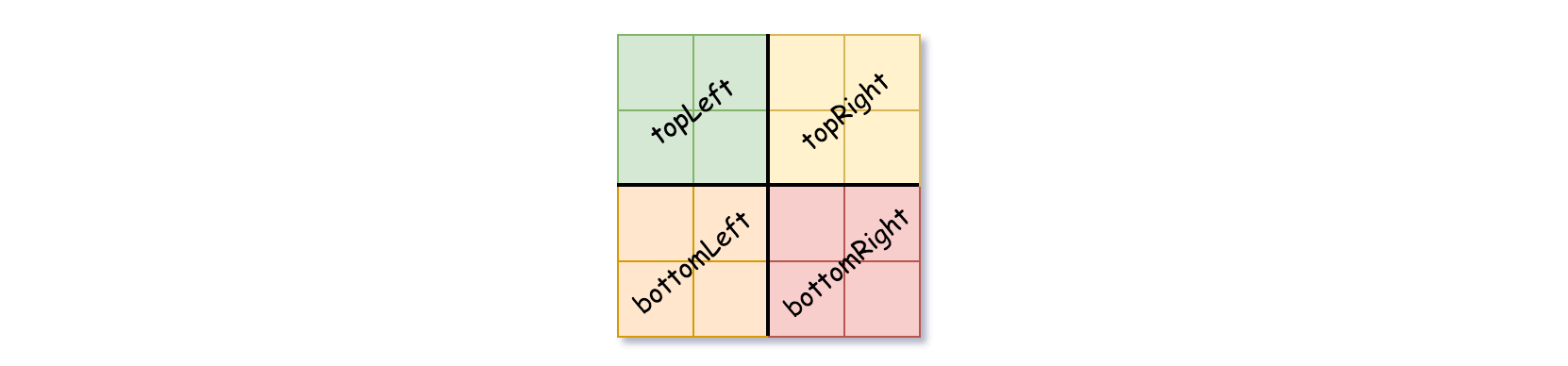
如果当前网格的值相同（即，全为 0 或者全为 1），将 isLeaf 设为 True ，将 val 设为网格相应的值，并将四个子节点都设为 Null 然后停止。
如果当前网格的值不同，将 isLeaf 设为 False，将 val 设为任意值，然后如下图所示，将当前网格划分为四个子网格。
使用适当的子网格递归每个子节点。

如果你想了解更多关于四叉树的内容，可以参考 wiki 。

四叉树格式：

输出为使用层序遍历后四叉树的序列化形式，其中 null 表示路径终止符，其下面不存在节点。

它与二叉树的序列化非常相似。唯一的区别是节点以列表形式表示 [isLeaf, val] 。

如果 isLeaf 或者 val 的值为 True ，则表示它在列表 [isLeaf, val] 中的值为 1 ；如果 isLeaf 或者 val 的值为 False ，则表示值为 0 。

示例1：

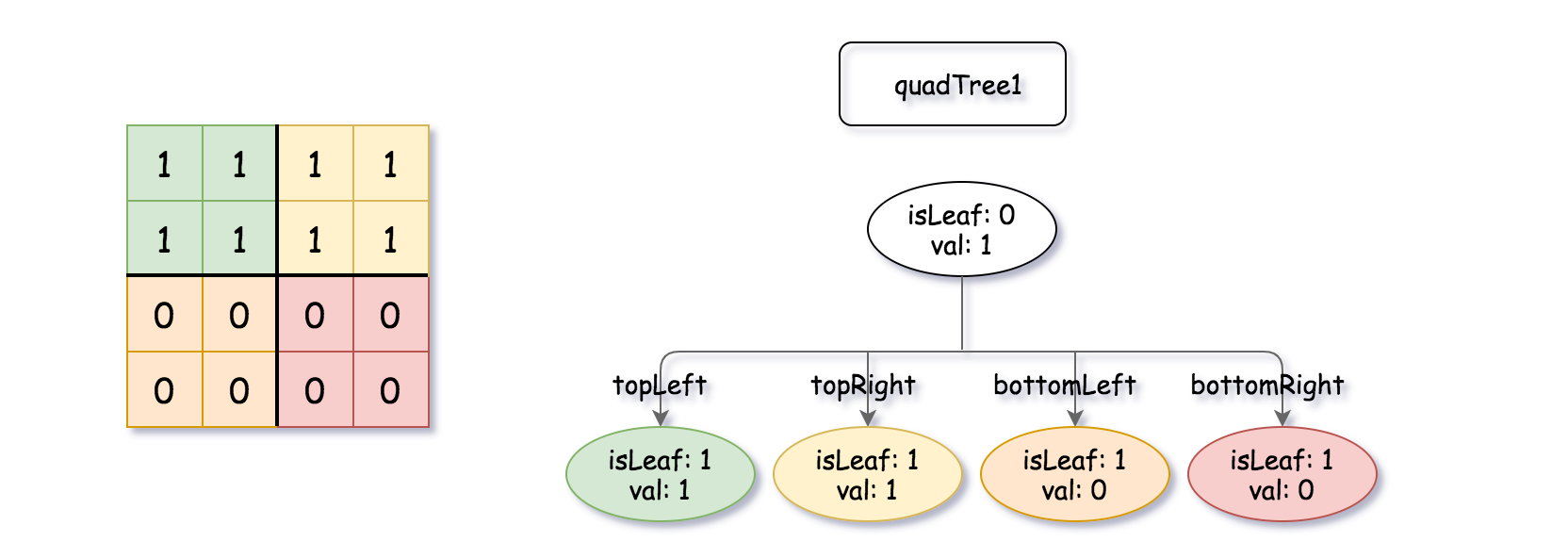
https://assets.leetcode.com/uploads/2020/02/11/qt1.png

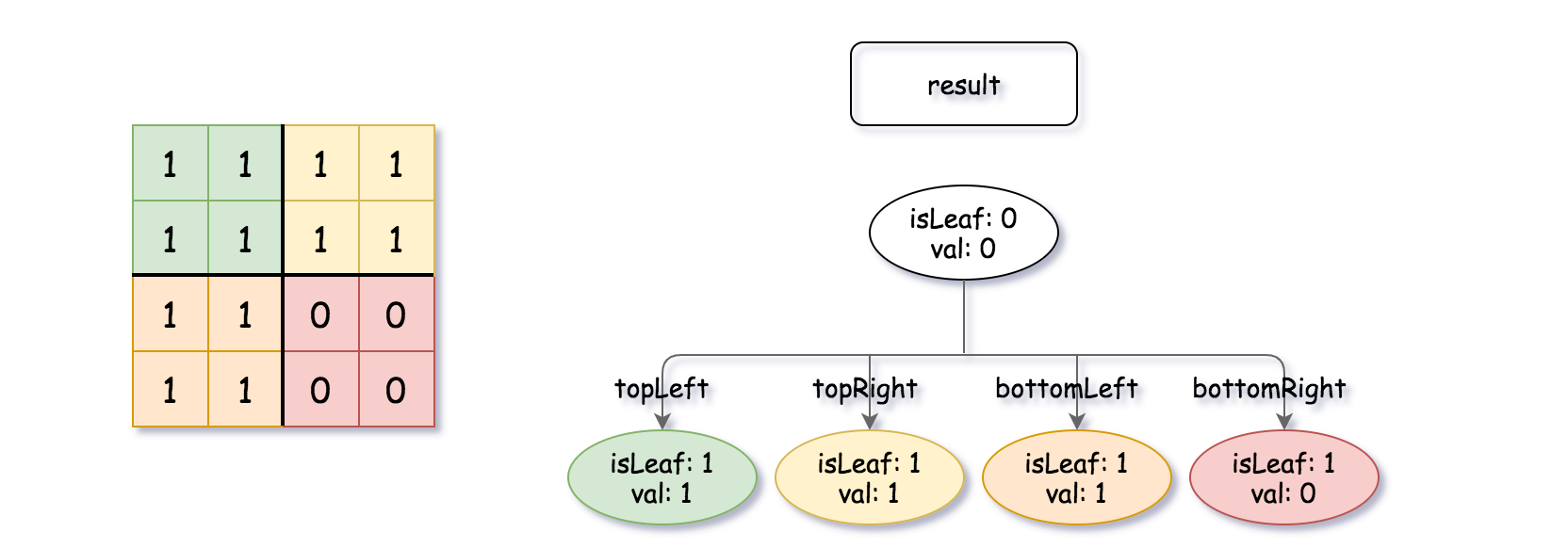
输入：quadTree1 = [[0,1],[1,1],[1,1],[1,0],[1,0]]
, quadTree2 = [[0,1],[1,1],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
输出：[[0,0],[1,1],[1,1],[1,1],[1,0]]
解释：quadTree1 和 quadTree2 如上所示。由四叉树所表示的二进制矩阵也已经给出。
如果我们对这两个矩阵进行按位逻辑或运算，则可以得到下面的二进制矩阵，由一个作为结果的四叉树表示。
注意，我们展示的二进制矩阵仅仅是为了更好地说明题意，你无需构造二进制矩阵来获得结果四叉树。

提示

quadTree1 和 quadTree2 都是符合题目要求的四叉树，每个都代表一个 n * n 的矩阵。
n == 2^x ，其中 0 <= x <= 9.

题解

首先对于或操作，有 $a\mid 1=1$ 和 $a\mid 0=a$，其中 $a=0,1$
使用分治算法解决，设当前遍历的两个结点分别为 $qt1$ 和 $qt2$ 有如下几种情况：

$qt1$ 是叶子结点：
- $qt1$ 的值为 true，$qt1\mid qt2=1$，即之后的结点值都为 true
- $qt1$ 的值为 false，$qt1\mid qt2=qt2$，即之后的结点值与 $qt2$ 相同。
$qt2$ 是叶子结点：
- $qt2$ 的值为 true，$qt1\mid qt2=1$，即之后的结点值都为 true
- $qt2$ 的值为 false，$qt1\mid qt2=qt2$，即之后的结点值与 $qt1$ 相同。
$qt1$ 和 $qt2$ 都不是叶子结点：
- 划分成四个子问题，即分成左上、右上、左下、右下。
- 合并：如果上述四个子问题得到的所有结果为值相同的叶子结点，那么可以合并成一个叶子结点；如果值不相同，那么需要新建一个结点，其四个子结点为上述四个子问题的结点。

代码

class Solution {
public:
    Node* intersect(Node* qt1, Node* qt2) {
        if (qt1->isLeaf) {
            if (qt1->val) {
                return new Node(true, true);
            }
            return new Node(qt2->val, qt2->isLeaf, qt2->topLeft, qt2->topRight, qt2->bottomLeft, qt2->bottomRight);
        }
        if (qt2->isLeaf) {
            if (qt2->val) {
                return new Node(true, true);
            }
            return new Node(qt1->val, qt1->isLeaf, qt1->topLeft, qt1->topRight, qt1->bottomLeft, qt1->bottomRight);
        }
        Node* a = intersect(qt1->topLeft, qt2->topLeft);
        Node* b = intersect(qt1->topRight, qt2->topRight);
        Node* c = intersect(qt1->bottomLeft, qt2->bottomLeft);
        Node* d = intersect(qt1->bottomRight, qt2->bottomRight);
        bool isLeaf = a->isLeaf && b->isLeaf && c->isLeaf && d->isLeaf;
        bool val = a->val == b->val && a->val == c->val && a->val == d->val;
        if (isLeaf && val) {
            return new Node(a->val, true);
        }
        return new Node(false, false, a, b, c, d);
    }
};

复杂度分析

时间复杂度：根据主定理
$$
T(n) = a T\left(\frac{n}{b}\right)＋f(n)\qquad \forall n > b
$$
$T (n) = {\begin{cases} Θ (n^{\log_{b} a}) & f (n) = O (n^{\log_{b} a - ϵ}) \\ Θ (f (n)) & f (n) = Ω (n^{\log_{b} a + ϵ}) \\ Θ (n^{\log_{b} a} \log^{k + 1} n) & f (n) = Θ (n^{\log_{b} a} \log^{k} n), k \geq 0 \end{cases}$
其中，原问题的子问题个数为$a=4$个，每个子问题的规模为原问题的一半$b=2$，即$\frac{n}{2}\times\frac{n}{2}$，每次递归带来的额外复杂度 $f(n^d)=O(1)$，可得总体复杂度 $O(n^2)$。
空间复杂度：$O(\log{n})$，为递归栈空间