LeetCode515. 在每个树行中找最大值

题目描述

本题目来自LeetCode上的『515. 在每个树行中找最大值』

给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。

示例1：

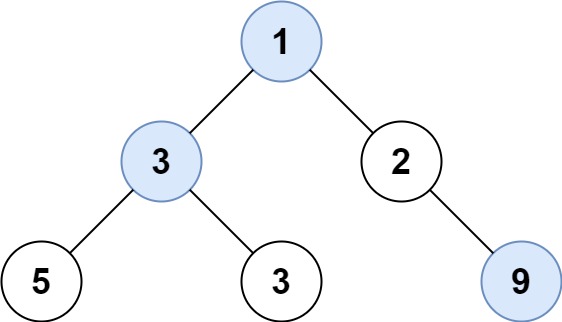
输入: root = [1,3,2,5,3,null,9]
输出: [1,3,9]

提示

二叉树的节点个数的范围是 [0,10^4]
-2^31 <= Node.val <= 2^31 - 1

题解1 - 深度优先搜索

将队列中所有的结点全部拿出来一次性遍历，即可保证每次循环都是新的一层。

代码

class Solution {
public:
    vector<int> largestValues(TreeNode* root) {
        if (root == nullptr) {
            return {};
        }
        vector<int> ans;
        queue<TreeNode*> q;
        q.emplace(root);
        while (!q.empty()) {
            int maxVal = INT_MIN;
            for (int i = q.size(); i > 0; --i) {
                TreeNode* p = q.front();
                q.pop();
                maxVal = max(maxVal, p->val);
                if (p->left) {
                    q.emplace(p->left);
                }
                if (p->right) {
                    q.emplace(p->right);
                }
            }  
            ans.emplace_back(maxVal);
        }
        return ans;
    }
};

复杂度分析

时间复杂度：$O(n)$
空间复杂度：$O(n)$

题解2 - 使用标记区分层次

使用BFS，在每一层的第一个结点入队前先入队一个空结点，这样每次遍历到空结点时，就表示上一层已经遍历结束。为了防止重复加入空结点，设置一个变量 isNewLine 来记录是否已经为下一层设置空结点。

代码

class Solution {
public:
    vector<int> largestValues(TreeNode* root) {
        if (root == nullptr) {
            return {};
        }
        vector<int> ans;
        int maxVal = INT_MIN;
        bool isNewLine = true;
        queue<TreeNode*> q;
        q.emplace(root);
        while (!q.empty()) {
            TreeNode* p = q.front();
            q.pop();
            if (p == nullptr) {
                ans.emplace_back(maxVal);
                maxVal = INT_MIN;
                isNewLine = true;
                continue;
            }
            maxVal = max(maxVal, p->val);
            if (isNewLine) {
                q.emplace(nullptr);
                isNewLine = false;
            }
            if (p->left) {
                q.emplace(p->left);
            }
            if (p->right) {
                q.emplace(p->right);
            }
        }
        return ans;
    }
};