LeetCode1252. 奇数值单元格的数目

题目描述

本题目来自LeetCode上的『1252. 奇数值单元格的数目』

给你一个 m x n 的矩阵，最开始的时候，每个单元格中的值都是 0。

另有一个二维索引数组 indices，indices[i] = [ri, ci] 指向矩阵中的某个位置，其中 ri 和 ci 分别表示指定的行和列（从 0 开始编号）。

对 indices[i] 所指向的每个位置，应同时执行下述增量操作：

ri 行上的所有单元格，加 1 。
ci 列上的所有单元格，加 1 。

给你 m、n 和 indices 。请你在执行完所有 indices 指定的增量操作后，返回矩阵中 奇数值单元格 的数目。

示例1：

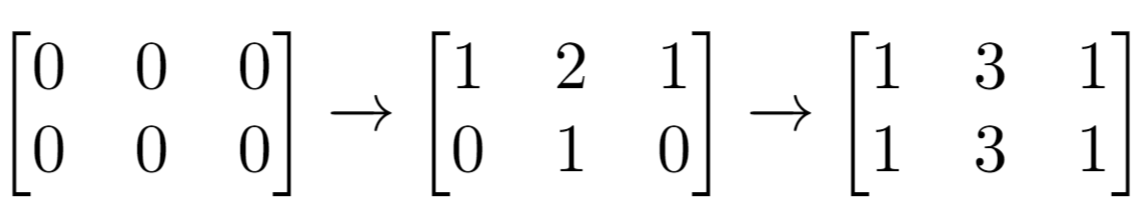
https://assets.leetcode-cn.com/aliyun-lc-upload/uploads/2019/11/06/e1.png

输入：m = 2, n = 3, indices = [[0,1],[1,1]]
输出：6
解释：最开始的矩阵是 [[0,0,0],[0,0,0]]。
第一次增量操作后得到 [[1,2,1],[0,1,0]]。
最后的矩阵是 [[1,3,1],[1,3,1]]，里面有 6 个奇数。

提示

1 <= m, n <= 50
1 <= indices.length <= 100
0 <= ri < m
0 <= ci < n

进阶：你可以设计一个时间复杂度为 O(n + m + indices.length) 且仅用 O(n + m) 额外空间的算法来解决此问题吗？

题解

令两个数组 $rowCnt$ 和 $colCnt$ 分别记录每一行和每一列加 1 的次数。

不失一般性，可以先对所有的行加 1，再对所有列加 1。

对于所有的行，若 $rowCnt[i]$ 为奇数，表示此时对应行的所有元素都为奇数，设 $oddRow$ 为 $rowCnt$ 中奇数的个数，设 $evenRow$ 为 $rowCnt$ 中偶数的个数，此时整个矩阵奇数的个数为 $ans=oddRow\times n$。

对于所有的列，每一列有 $oddRow$ 个奇数，若 $colCnt[i]$ 为奇数，表示此列所有的数奇偶性反转，此时该列有 $oddRow$ 个偶数，$evenRow$ 个奇数，此时整个矩阵奇数的个数为 $ans=ans-oddRow+evenRow$，遍历 $colCnt$，计算得到结果。

代码

class Solution {
public:
    int oddCells(int m, int n, vector<vector<int>>& indices) {
        vector<int> rowCnt(m, 0);
        vector<int> colCnt(n, 0);
        for (const auto& index: indices) {
            ++rowCnt[index[0]];
            ++colCnt[index[1]];
        }
        int oddRow = 0;
        for (const auto& row: rowCnt) {
            if (row & 1) ++oddRow;
        }
        int evenRow = m - oddRow, diff = evenRow - oddRow;
        int ans = oddRow * n;
        for (const auto& col: colCnt) {
            if (col & 1) ans += diff;
        }
        return ans;
    }
};