LeetCode1217. 玩筹码

题目描述

本题目来自LeetCode上的『1217. 玩筹码』

有 n 个筹码。第 i 个筹码的位置是 position[i] 。

我们需要把所有筹码移到同一个位置。在一步中，我们可以将第 i 个筹码的位置从 position[i] 改变为:

position[i] + 2 或 position[i] - 2 ，此时 cost = 0
position[i] + 1 或 position[i] - 1 ，此时 cost = 1

返回将所有筹码移动到同一位置上所需要的 最小代价 。

示例1：

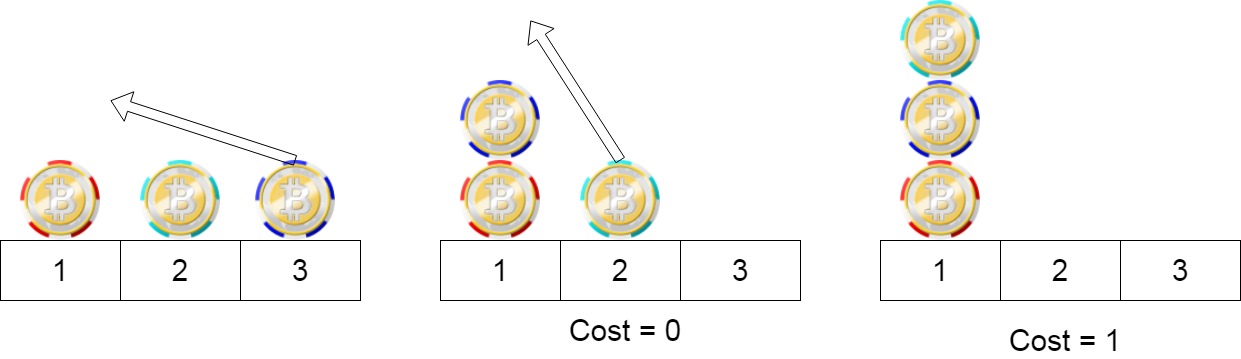
输入：position = [1,2,3]
输出：1
解释：第一步:将位置3的筹码移动到位置1，成本为0。
第二步:将位置2的筹码移动到位置1，成本= 1。
总成本是1。

提示

1 <= chips.length <= 100
1 <= chips[i] <= 10^9

题解

有以下贪心策略：

筹码在相同奇偶性的位置上移动代价为零，因此可以在具有相同奇偶性位置上任意移动筹码。
如果筹码全在偶数位或者奇数位，那么最终代价为零。
否则，将奇数位的筹码全部移动到同一个奇数位上，偶数位的筹码全部移动到同一个偶数位上，因为偶数位和奇数位之间的距离为奇数，因此至少需要一次代价为 1 的移动，我们移动数量最少的那一堆筹码即可。

根据上述贪心策略，分别统计奇偶数的个数并返回其中最小的那个。

代码

class Solution {
public:
    int minCostToMoveChips(vector<int>& position) {
        int n = position.size();
        int oddCnt = 0, evenCnt = 0;

        for (int i = 0; i < n; ++i) {
            if (position[i] & 1) ++oddCnt;
            else ++evenCnt;
        }

        return min(oddCnt, evenCnt);
    }
};

或者

class Solution {
public:
    int minCostToMoveChips(vector<int>& position) {
        size_t cnt = count_if(position.begin(), position.end(), [](int i) { return i & 1; });
        return min(cnt, position.size() - cnt);
    }
};